Nonlinear Inversion Authors
Affiliations
Douglas Oldenburg
University of British Columbia
University of British Columbia
February 10, 2021
In the previous sections we showed how observations from a linear system can be inverted to generate a candidate for the underlying model m m m d = F [ m ] d=F[m] d = F [ m ]
Linear Inversion Review ¶ The inverse problem is set to minimize the objective function ϕ = ϕ d + β ϕ m \phi=\phi_d+\beta\phi_m ϕ = ϕ d + β ϕ m ϕ d = ∑ j = 1 N ( F j ( m ) − d j o b s ε j ) 2 \phi_d=\sum^N_{j=1}\left(\frac{\mathcal{F}_j(m)-d_j^{obs}}{\varepsilon_j}\right)^2 ϕ d = ∑ j = 1 N ( ε j F j ( m ) − d j o b s ) 2 d = G m \mathbf{d}=\mathbf{Gm} d = Gm ∫ v ( m − m r e f ) 2 d v \int_v\left(m-m_{ref}\right)^2dv ∫ v ( m − m re f ) 2 d v
Non-linear Inversion ¶ The inverse problem becomes non-linear in any of the following cases:
when the forward operation F [ m ] \mathcal{F}[m] F [ m ] when the data misfit ϕ d \phi_d ϕ d l 2 l_2 l 2 ∑ ∣ F i [ m ] − d i ε i ∣ \sum\left|\frac{\mathcal{F}_i[m]-d_i}{\varepsilon_i}\right| ∑ ∣ ∣ ε i F i [ m ] − d i ∣ ∣ when the model objective function is not quadratic Forward ¶ The forward problem is defined as d = F [ m ] d=\mathcal{F}[m] d = F [ m ] d = G m \mathbf{d}=\mathbf{Gm} d = Gm F [ a m 1 + b m 1 ] ≠ a F [ m 1 ] + b F [ m 2 ] \mathcal{F}[am_1+bm_1] \neq a\mathcal{F}[m_1]+b\mathcal{F}[m_2] F [ a m 1 + b m 1 ] = a F [ m 1 ] + b F [ m 2 ]
Inverse Problem ¶ We now solve an optimization problem to minimize the objective function ϕ ( m ) = ϕ d + β ϕ m ( m ) \phi(m)=\phi_d+\beta\phi_m(m) ϕ ( m ) = ϕ d + β ϕ m ( m )
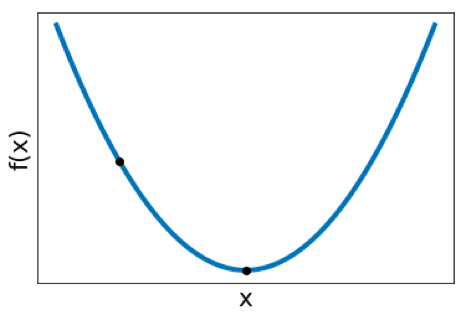
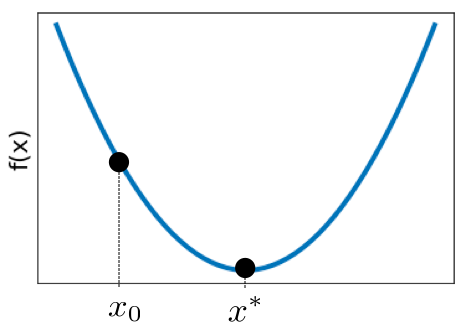
Non-linear Optimization ¶ Consider a single variable x x x f f f f ( x ) f(x) f ( x ) f \mathcal{f} f
f ( x ) = 1 4 x 2 − 3 x + 9 = ( 1 2 x − 3 ) 2 \begin{aligned} f(x)&=\frac{1}{4}x^2-3x+9\\ &=\left(\frac{1}{2}x-3\right)^2 \end{aligned} f ( x ) = 4 1 x 2 − 3 x + 9 = ( 2 1 x − 3 ) 2 then we can take the derivative, set it equal to 0, and solve for x x x
f ′ ( x ) = ( 1 2 x − 3 ) = 0 x = 6 \begin{aligned} f\prime(x)&=\left(\frac{1}{2}x-3\right) \\ &=0\\ x&=6 \end{aligned} f ′ ( x ) x = ( 2 1 x − 3 ) = 0 = 6 We know that the minimum of f ′ ( x ) = 0 f{\prime}(x)=0 f ′ ( x ) = 0 f ′ ′ ( x ) > 0 f\prime\prime(x)>0 f ′′ ( x ) > 0
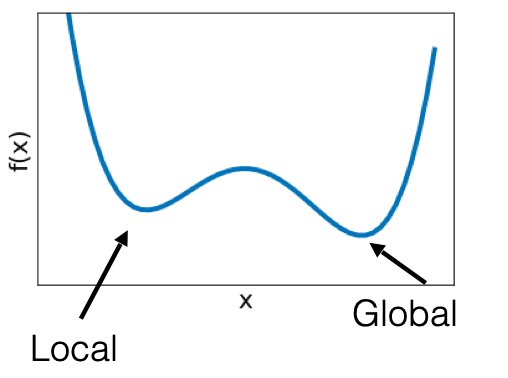
Suppose we have a function that is not quadratic, such as
f ( x ) = ( 1 2 x − 3 ) 2 + a x 3 + b x 4 f(x)=\left(\frac{1}{2}x-3\right)^2+ax^3+bx^4 f ( x ) = ( 2 1 x − 3 ) 2 + a x 3 + b x 4 where there are now multiple minimums, as shown below.
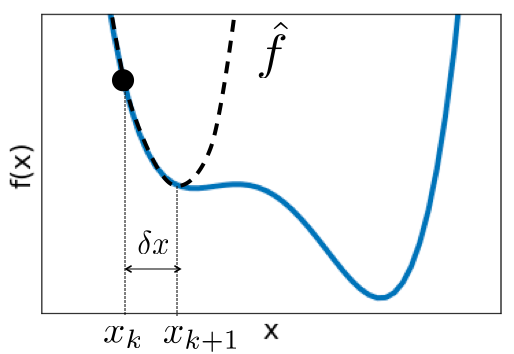
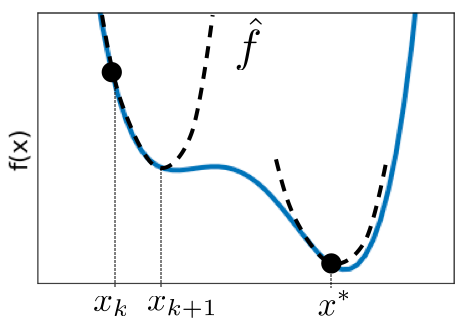
Newton’s Method ¶ Begin with an initial guess of the minimum, x k x_k x k f \mathcal{f} f
Approximate f \mathcal{f} f f ^ \hat{\mathcal{f}} f ^ x k x_k x k δ x \delta x δ x f ^ \hat{\mathcal{f}} f ^ f ^ \hat{\mathcal{f}} f ^
f ^ ( x k + δ x ) = f ( x k ) + f ′ ( x k ) δ x + 1 2 f ′ ′ ( x k ) δ x 2 + O ( δ x 3 ) f ^ ′ = f ′ ( x k ) δ x + 1 2 f ′ ′ ( x k ) δ x 2 + O ( δ x 3 ) = 0 f ′ ′ ( x k ) δ x = − f ′ ( x k ) δ x = − f ′ ( x k ) f ′ ′ ( x k ) \begin{aligned}\hat{\mathcal{f}}(x_k+\delta x)&=\mathcal{f}(x_k)+\mathcal{f}\prime (x_k)\delta x+\frac{1}{2}f\prime\prime (x_k)\delta x^2 +\cancel{\mathcal{O}(\delta x^3)}\\ \hat{\mathcal{f}}\prime&=\mathcal{f}\prime (x_k)\delta x+\frac{1}{2}f\prime\prime (x_k)\delta x^2+\cancel{\mathcal{O}(\delta x^3)}\\ &=0\\ \mathcal{f}\prime\prime(x_k)\delta x&=-\mathcal{f}\prime(x_k)\\ \delta x&=-\frac{\mathcal{f}\prime(x_k)}{\mathcal{f}\prime\prime(x_k)}\end{aligned} f ^ ( x k + δ x ) f ^ ′ f ′′ ( x k ) δ x δ x = f ( x k ) + f ′ ( x k ) δ x + 2 1 f ′′ ( x k ) δ x 2 + O ( δ x 3 ) = f ′ ( x k ) δ x + 2 1 f ′′ ( x k ) δ x 2 + O ( δ x 3 ) = 0 = − f ′ ( x k ) = − f ′′ ( x k ) f ′ ( x k )
Update the guess x k + 1 = x k + δ x x_{k+1}=x_k+\delta x x k + 1 = x k + δ x
Quadratic converge: ∣ x k + 1 − x ∗ ∣ < c ∣ x k − x ∗ ∣ 2 \left|x_{k+1}-x^*\right|<c\left|x_k-x^*\right|^2 ∣ x k + 1 − x ∗ ∣ < c ∣ x k − x ∗ ∣ 2
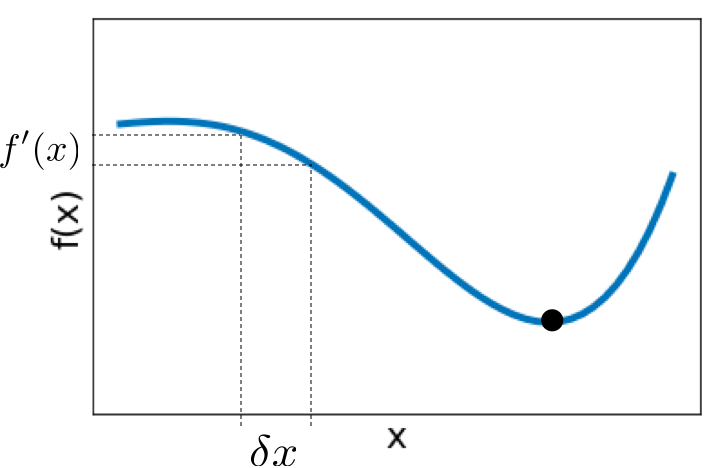
Things can go wrong with δ x = − f ′ ( x k ) f ′ ′ ( x k ) \delta x=-\frac{\mathcal{f}\prime(x_k)}{\mathcal{f}\prime\prime(x_k)} δ x = − f ′′ ( x k ) f ′ ( x k )
If we move in the wrong direction, we likely have negative curvature ( − f ′ ′ ( x ) ) \left(-\mathcal{f}\prime\prime(x)\right) ( − f ′′ ( x ) ) δ x = c f ′ ( x ) \delta x = c\mathcal{f}\prime (x) δ x = c f ′ ( x ) c c c c c c ∣ f ( x + δ x ) − f ( x ) ∣ > ε \left|\mathcal{f}(x+\delta x)-\mathcal{f}(x)\right|>\varepsilon ∣ f ( x + δ x ) − f ( x ) ∣ > ε f ′ ′ ( x ) \mathcal{f}\prime\prime(x) f ′′ ( x ) x k + 1 = x k + α δ x x_{k+1}=x_k+\alpha\delta x x k + 1 = x k + α δ x α < 1 \alpha<1 α < 1
Convergence Conditions ¶ f ′ ( x ) < \mathcal{f}\prime(x)< f ′ ( x ) < ∥ δ x ∥ < \|\delta x\|< ∥ δ x ∥ < f ′ ′ ( x ) > 0 \mathcal{f}\prime\prime (x)>0 f ′′ ( x ) > 0 Summary (Newton’s Method) ¶ Linear:
solution in one step f ′ ′ ( x ) δ x = − f ′ ( x ) \mathcal{f}\prime\prime(x)\delta x=-\mathcal{f}\prime(x) f ′′ ( x ) δ x = − f ′ ( x ) x ∗ = − f ′ ( x ) f ′ ′ ( x ) x^*=-\frac{\mathcal{f}\prime(x)}{\mathcal{f}\prime\prime(x)} x ∗ = − f ′′ ( x ) f ′ ( x ) Non-linear
iterate to convergence f ′ ′ ( x k ) δ x = − f ′ ( x k ) \mathcal{f}\prime\prime(x_k)\delta x=-\mathcal{f}\prime(x_k) f ′′ ( x k ) δ x = − f ′ ( x k ) δ x = − f ′ ( x k ) f ′ ′ ( x k ) \delta x=-\frac{\mathcal{f}\prime(x_k)}{\mathcal{f}\prime\prime(x_k)} δ x = − f ′′ ( x k ) f ′ ( x k ) x k + 1 = x k + α δ x , α < 1 x_{k+1}=x_k+\alpha\delta x, ~ \alpha<1 x k + 1 = x k + α δ x , α < 1 Multivariate functions ¶ Minimize ϕ ( m ) , m ∈ { m 1 , m 2 , … , m M } \phi(m), ~ m\in\{m_1, m_2, \dots, m_M\} ϕ ( m ) , m ∈ { m 1 , m 2 , … , m M } Taylor expansion of ϕ ( m ) \phi(m) ϕ ( m ) ϕ ( m + δ m ) = ϕ ( m ) + ( ∇ m ϕ ( m ) ) T δ m + 1 2 δ m T ∇ m ( ∇ m ϕ ( m ) ) T δ m + O ( δ m 3 ) \phi(m+\delta m)=\phi(m)+(\nabla_m\phi(m))^T\delta m+\frac{1}{2}\delta m^T\nabla_m(\nabla_m\phi(m))^T\delta m+\mathcal{O}(\delta m^3) ϕ ( m + δ m ) = ϕ ( m ) + ( ∇ m ϕ ( m ) ) T δ m + 2 1 δ m T ∇ m ( ∇ m ϕ ( m ) ) T δ m + O ( δ m 3 ) Note the similarity to single variablef ( x + δ x ) = f ( x ) + f ′ ( x ) δ x + 1 2 f ′ ′ ( x ) δ x 2 + O ( δ x 3 ) \mathcal{f}(x+\delta x)=\mathcal{f}(x)+\mathcal{f}\prime(x)\delta x+\frac{1}{2}\mathcal{f}\prime\prime(x)\delta x^2+\mathcal{O}(\delta x^3) f ( x + δ x ) = f ( x ) + f ′ ( x ) δ x + 2 1 f ′′ ( x ) δ x 2 + O ( δ x 3 ) Define the Gradient
g ( m ) = ∇ m ϕ , g ∈ R M = ( ∂ ϕ ∂ m 1 ⋮ ∂ ϕ ∂ m M ) \begin{aligned} g(m)&=\nabla_m\phi, ~ g\in \R^M \\ &=\begin{pmatrix} \frac{ \partial \phi}{\partial m_1} \\ \vdots \\ \frac{ \partial \phi}{\partial m_M} \end{pmatrix}\end{aligned} g ( m ) = ∇ m ϕ , g ∈ R M = ⎝ ⎛ ∂ m 1 ∂ ϕ ⋮ ∂ m M ∂ ϕ ⎠ ⎞ The minimum of the gradient is defined such that g ( m ∗ ) = 0 g(m^*)=0 g ( m ∗ ) = 0
Define the Hessian (symmetric matrix)
H ( m ) = ∇ m ∇ m T ϕ , H ∈ R M × M = ( ∂ 2 ϕ ∂ m 1 2 ∂ 2 ϕ ∂ m 1 ∂ m 2 ⋯ ∂ 2 ϕ ∂ m 1 ∂ m M ∂ 2 ϕ ∂ m 2 ∂ m 1 ∂ 2 ϕ ∂ m 2 2 ⋯ ∂ 2 ϕ ∂ m 2 ∂ m M ⋮ ⋮ ⋱ ⋮ ∂ 2 ϕ ∂ m M ∂ m 1 ∂ 2 ϕ ∂ m M ∂ m 2 ⋯ ∂ 2 ϕ ∂ m M 2 ) H i , j = ∂ 2 ϕ ∂ m i ∂ m j \begin{aligned} H(m)&=\nabla_m\nabla^T_m\phi, ~H\in\R^{M\times M} \\ &=\begin{pmatrix} \frac{\partial^2 \phi}{\partial m_1^2} & \frac{\partial^2 \phi}{\partial m_1\partial m_2} & \cdots & \frac{\partial^2 \phi}{\partial m_1 \partial m_M} \\ \frac{\partial^2 \phi}{\partial m_2\partial m_1} & \frac{\partial^2 \phi}{\partial m_2^2} & \cdots & \frac{\partial^2 \phi}{\partial m_2\partial m_M} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 \phi}{\partial m_M\partial m_1} & \frac{\partial^2 \phi}{\partial m_M\partial m_2} & \cdots & \frac{\partial^2 \phi}{\partial m_M^2}\end{pmatrix} \\ H_{i,j}&=\frac{\partial^2\phi}{\partial m_i \partial m_j}\end{aligned} H ( m ) H i , j = ∇ m ∇ m T ϕ , H ∈ R M × M = ⎝ ⎛ ∂ m 1 2 ∂ 2 ϕ ∂ m 2 ∂ m 1 ∂ 2 ϕ ⋮ ∂ m M ∂ m 1 ∂ 2 ϕ ∂ m 1 ∂ m 2 ∂ 2 ϕ ∂ m 2 2 ∂ 2 ϕ ⋮ ∂ m M ∂ m 2 ∂ 2 ϕ ⋯ ⋯ ⋱ ⋯ ∂ m 1 ∂ m M ∂ 2 ϕ ∂ m 2 ∂ m M ∂ 2 ϕ ⋮ ∂ m M 2 ∂ 2 ϕ ⎠ ⎞ = ∂ m i ∂ m j ∂ 2 ϕ The minimum of the Hessian is defined such that H ( m ∗ ) H(m^*) H ( m ∗ )
Finding a Solution ¶ Begin with an initial model m ( k ) m^{(k)} m ( k ) Solve H ( m ( k ) ) δ m = − g ( m ( k ) ) , c.f. { f ′ ′ ( x ) δ x = f ′ ( x ) } H\left(m^{(k)}\right)\delta m=-g\left(m^{(k)}\right), ~ \text{c.f.}\{\mathcal{f}\prime\prime(x)\delta x=\mathcal{f}\prime(x)\} H ( m ( k ) ) δ m = − g ( m ( k ) ) , c.f. { f ′′ ( x ) δ x = f ′ ( x )} Update the model m ( k + 1 ) = m ( k ) + α δ m m^{(k+1)}=m^{(k)}+\alpha\delta m m ( k + 1 ) = m ( k ) + α δ m Our Inversion ¶ Minimize
ϕ ( m ) = 1 2 ∣ ∣ F [ m ] − d o b s ∣ ∣ 2 + β 2 ∥ m ∥ 2 \phi(m) = \frac{1}{2} \left|\left| \mathcal{F}[m]-d^{obs}\right|\right|^2 + \frac{\beta}{2} \| m \|^2 ϕ ( m ) = 2 1 ∣ ∣ ∣ ∣ F [ m ] − d o b s ∣ ∣ ∣ ∣ 2 + 2 β ∥ m ∥ 2 Gradient
g ( m ) = ∇ m ϕ = J T ( F [ m ] − d o b s ) + β m \begin{aligned} g(m) &= \nabla_m \phi \\ &= J^T \left( \mathcal{F}[m]-d^{obs}\right) + \beta m \end{aligned} g ( m ) = ∇ m ϕ = J T ( F [ m ] − d o b s ) + β m Sensitivity:
∇ m F ( m ) = J J i j = ∂ F i [ m ] ∂ m j \begin{aligned} \nabla_m\mathcal{F}(m)&=J\\ J_{ij}&=\frac{\partial \mathcal{F}_i[m]}{\partial m_j} \end{aligned} ∇ m F ( m ) J ij = J = ∂ m j ∂ F i [ m ] Hessian:
H ( m ) = ∇ m g ( m ) = J T J + ( ∇ m J ) T ( F [ m ] − d o b s ) + β \begin{aligned} H(m) &= \nabla_m g(m) \\ &= J^T J + \cancel{ (\nabla_m J)^T \big(\mathcal{F}[m]-d^{obs}\big)} +\beta\end{aligned} H ( m ) = ∇ m g ( m ) = J T J + ( ∇ m J ) T ( F [ m ] − d o b s ) + β *we neglect the second term
Final:
H δ m = − g ↓ ( J T J + β ) δ m = − ( J T δ d + β m ) δ d = F [ m ] − d o b s \begin{aligned} H\delta m &= -g\\ & \downarrow \\ \left(J^TJ+\beta\right)\delta m &=-\left(J^T\delta d+\beta m\right) \\ \delta d &= \mathcal{F}[m]-d^{obs}\end{aligned} Hδ m ( J T J + β ) δ m δ d = − g ↓ = − ( J T δ d + β m ) = F [ m ] − d o b s Linear v. Non-linear ¶ Non-linear Problem ( F [ m ] = d ) \left(\mathcal{F}[m]=d\right) ( F [ m ] = d )
( J T J + β ) δ m = − ( J T δ d + β m ) , δ d = F [ m ] − d o b s \left(J^TJ+\beta\right)\delta m=-\left(J^T\delta d+\beta m\right), ~\delta d=\mathcal{F}[m]-d^{obs} ( J T J + β ) δ m = − ( J T δ d + β m ) , δ d = F [ m ] − d o b s Linear Problem ( G m = d ) (Gm=d) ( G m = d )
( G T G + β ) δ m = − ( G T d + β m ) \left(G^TG+\beta\right)\delta m=-\left(G^Td+\beta m\right) ( G T G + β ) δ m = − ( G T d + β m ) The sensitivity J J J J δ m = δ d J\delta m=\delta d J δ m = δ d
General Algorithm ¶ Minimize ϕ = ϕ d + β ϕ m \phi=\phi_d+\beta\phi_m ϕ = ϕ d + β ϕ m
initialize the model and β: m ( 0 ) , β ( 0 ) m^{(0)}, ~\beta^{(0)} m ( 0 ) , β ( 0 ) Until convergence is reached, iterate through the following:H δ m = − g H\delta m=-g Hδ m = − g m ( k + 1 ) = m ( k ) + α δ m m^{(k+1)}=m^{(k)}+\alpha\delta m m ( k + 1 ) = m ( k ) + α δ m β ( k + 1 ) = β ( k ) γ \beta^{(k+1)}=\frac{\beta^{(k)}}{\gamma} β ( k + 1 ) = γ β ( k ) There are a variety of ways to solve the system and selecting β beyond a line search and the cooling rate.
Summary ¶ ϕ ( m ) = 1 2 ∣ ∣ F [ m ] − d o b s ∣ ∣ 2 + β 2 ∣ ∣ m ∣ ∣ 2 \phi(m)=\frac{1}{2}\left|\left|\mathcal{F}[m]-d^{obs}\right|\right|^2+\frac{\beta}{2}\left|\left|m\right|\right|^2 ϕ ( m ) = 2 1 ∣ ∣ ∣ ∣ F [ m ] − d o b s ∣ ∣ ∣ ∣ 2 + 2 β ∣ ∣ m ∣ ∣ 2 Linear
Forward: d = G m d=Gm d = G m Inverse: Non-linear
d = F [ m ] d=\mathcal{F}[m] d = F [ m ] ( J T J + β ) δ m = − ( J T δ d + β m ) \left(J^TJ+\beta\right)\delta m=-\left(J^T\delta d+\beta m\right) ( J T J + β ) δ m = − ( J T δ d + β m ) δ d = F [ m ] − d o b s \delta d=\mathcal{F}[m]-d^{obs} δ d = F [ m ] − d o b s m ( k + 1 ) = m ( k ) + α m m^{(k+1)}=m^{(k)}+\alpha m m ( k + 1 ) = m ( k ) + α m All understanding from the linear problem is valid for the non-linear problem